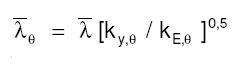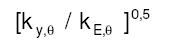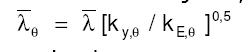Procedimiento de Cálculo de la Temperatura Crítica para Estructuras Metálicas
De Construmatica

|
Nota: Este artículo ha sido creado gracias a APTA en el marco del Programa de Afiliados de la Construpedia. El contenido está disponible en el sitio web de APTA.
¡Atención! Esté artículo está sujeto a Derecho de Autor. |
|---|
Estamos trabajando en este artículo.
En el cálculo práctico, el método de temperatura crítica puede ser aplicado según las etapas siguientes:
- En primer lugar, es necesario determinar el efecto de las acciones en situación de incendio E fi d
- En segundo lugar, conviene calcular la resistencia de cálculo Rd o el efecto de las acciones a temperatura normal E d
- En tercer lugar, el nivel de carga correspondiente puede ser obtenido utilizando ηfi, t = Efi,d /Rd
- Después, la tasa de utilización µ 0 puede ser fácilmente determinada con µ 0= ηfi,tγM,fi / γM dónde sólo un coeficiente parcial de γM es necesario.
- Finalmente la temperatura crítica es evaluada directamente con la relación indicada más arriba.
Es necesario prestar una atención particular al cálculo de tasas de utilización µ0 a partir del nivel de carga ηfi,t. La diferencia entre ellos consiste en el hecho de que la tasa de utilización µ0 es determinada en relación con la resistencia al fuego a un tiempo 0: R fi,d,o es decir a una temperatura normal pero con los coeficientes parciales γ M,fi, y en situación de incendio. En cambio, el nivel de carga ηfi, t es determinado utilizando Rd , la resistencia en estado límite en el redimensionamiento a temperatura normal, es decir con los coeficientes parciales correspondientes γ M que son en general diferentes de γM,fi.
El procedimiento puede ser iterativo en lugar de un cálculo directo, sea por ejemplo el casode un pilar de acero expuesto al fuego. Si el pilar es suficientemente corto para que no pandee, su resistencia a temperaturas elevadas puede ser calculada simplemente mediante N b,fi,t, Rd = AK y, θmax f y/ γM,fi.
En este caso la resistencia del pilar en función de la temperatura dependerá únicamente del factor de reducción relativo a la resistencia k y, θ puesto que los otros parámetros tienen valores fijos. Lo mismo ocurre en la tracción simple.
Sin embargo, cuando el pilar es esbelto de manera que hay riesgo de pandeo a temperaturas elevadas debe ser calculado mediante N b,fi,t,Rd = χ (λθ) AK y,θmax fy/ γM,fi.
En esas circunstancias la resistencia del pilar en función de la temperatura dependerá no sólo del factor de reducción relativo a la resistencia k y,θ sino también de la reducción debida al incendio ...λ θ que varía en función del factor de reducción relativo a la resistencia, a saber ky,θ y el factor de reducción relativo a su rigidez, es decir:
Por consiguiente no es posible obtener en un cálculo directo la temperatura crítica θ cr en función únicamente de K θ,y . Es un procedimiento iterativo simple, son necesarias 2 iteraciones como máximo para encontrar un valor preciso de θ cr en caso de problemas de estabilidad.
Se puede evitar el cálculo iterativo, tomando un valor fijado,del lado de la seguridad para
a fin de que:
no varíe con la temperatura; de este modo el cálculo directo de la temperatura crítica puede aplicarse incluso en el caso de elementos susceptibles de colapso por pérdida de inestabilidad.
Artículos Relacionados
- Calentamiento de la Sección de un Elemento de Acero
- Aplicación Práctica del Cálculo de Calentamiento de una Sección de Acero
- Noción de Temperatura Crítica en Estructuras de Acero no Protegidas