Diferencia entre las páginas «Cálculo de Estructuras de Acero: Caso de las Vigas» y «Cálculo de Estructuras de Acero: Caso de Esfuerzos Axiales (Columnas)»
De Construmatica
(Diferencia entre las páginas)
imported>112 |
|||
| Línea 3: | Línea 3: | ||
{{Área de Cálculo Acero}} | {{Área de Cálculo Acero}} | ||
= | =Los esfuerzos axiales (Pandeo de barras o columnas)= | ||
==Generalidades== | |||
En el análisis lineal de estructuras, a un aumento de las cargas exteriores corresponde un aumento proporcional de las deformaciones y de los esfuerzos internos. Sin embargo, se presentan casos en los que la aplicación de las cargas, aun siendo estas no muy grandes, modifican de tal forma la geometría del sistema, que aquella proporcionalidad deja de ser aplicable, y la estructura se deforma de una manera distinta de lo que correspondería a dichas cargas en el rango lineal, pudiendo incluso provocar su ''colapso''. A los valores de las cargas que provocan el colapso de la estructura, se les denominan '''cargas críticas de colapso'''. | |||
Cuando las deformaciones no son pequeñas, la posición de las cargas en la estructura deformada, no puede confundirse con la posición en la estructura sin deformar y por lo tanto, las ecuaciones de equilibrio deben ser planteadas ahora en la posición deformada, y no en la inicial. | |||
'' | Los conceptos de '''carga crítica''' y estabilidad del equilibrio pueden ponerse de manifiesto con gran facilidad mediante un caso sencillo, que además permitirá una generalización posterior. | ||
[[Imagen:Fig00.jpg|right|250px||]] | |||
Considérese el sistema mostrado en la figura adjunta. Un análisis de primer orden, planteando el equilibrio en la posición indeformada, indica que la barra está sometida a una compresión simple de valor <math>P</math>. | |||
En este caso la flecha <math>d</math> no puede despreciarse al lado de la excentricidad inicial <math>e</math>. El momento flector a lo largo del eje <math>x</math> para cualquier sección se expresará como: | |||
<math> | ::<math>M = -P.(d+e- y)</math> | ||
La ecuación general de la deformada –también llamada ''ecuación de la elástica''– se presenta así: | |||
::<math>\frac{d^2y}{dx^2} = -\frac{M}{E.I}.[1 + (\frac{dy}{dx})^2]^{3/2}</math> | |||
Aplicándola al caso particular en estudio, la integración analítica de esta ecuación, resuelta por ''Lagrange'', conduce a una solución complicada y de engorroso manejo. ''Schneider'' deduce para la máxima deformación: | |||
::<math>y_M = \sqrt{\frac{E.I}{P}}\sqrt{[\frac{P}{P_M} -1]-\frac{9}{4}[\frac{P}{P_M}-1]^2+\frac{31}{8}[\frac{P}{P_M}-1]^3- .... }</math> | |||
La | que no deja de ser todavía de manejo engorroso. Por esta razón, algunos autores prefieren la integración de la forma simplificada: | ||
::<math>\frac{d^2y}{dx^2} = -\frac{P.(d+e-y)}{E.I}</math> | |||
aduciendo que, en la práctica, el valor de: <math>[1 + (\frac{dy}{dx})^2]^{3/2}</math> es siempre despreciable. Esta hipótesis puede proporcionar resultados de cierto valor cualitativo y orientativo, si bien su validez numérica, por lo ya expresado, '''es muy discutible'''. Aceptada esta hipótesis, la integración de esta última expresión, conduce a: | |||
::<math>y=\frac{e.[1-cos(\sqrt{\frac{P}{E.I}}.x)]}{cos(\sqrt{\frac{P}{E.I}}.L)}</math> | |||
Cuando el valor de <math>\sqrt{\frac{P}{E.I}}.L \rightarrow \pi/2</math> | |||
en la ecuación anterior, la deformación <math>y</math> '''tiende a infinito''', lo que significa que la columna se ''colapsará'', es decir, su deformación aumentará hasta que se quede doblada sobre si misma. Antes de llegar a ello, la pieza de acero laminado habrá alcanzado su punto de fluencia, e iniciará una deformación plástica, pudiendo llegar a su límite de rotura. Aceptada esa hipótesis, la carga P que causará este colapso se deducirá de <math>\sqrt{\frac{P_C}{E.I}}.L = \pi/2</math> | |||
Al valor de la carga<math>P_C=\frac{\pi^2.E.I}{4.L^2}</math> se la denomina <math>Carga\;critica\;de\;Euler</math>. | |||
El momento flector máximo producido por esta carga, se presentará en el empotramiento, y valdrá, según se ha visto: | |||
::<math>M_{Max}=-P_C.(d+e)=-P_C.e.sec(\sqrt{\frac{P_C}{E.I}}.L)</math> | |||
===Observaciones a la definición de '''Carga Crítica'''=== | |||
La integración de la ecuación simplificada no representa, como ya se ha indicado, la solución exacta, ya que si la carga se acerca al valor crítico <math>P_C</math>, las deformaciones son importantes (se "acercan a infinito") y el término <math>[1 + (\frac{dy}{dx})^2]^{3/2}</math>no puede ser despreciado. Sin embargo, el resultado exacto de esa integración muestra que la conclusión obtenida en el caso particular anterior, es válida en su aspecto cualitativo y en efecto, cuando la carga toma un cierto valor –aunque inferior al anteriormente denominado ''crítico''– la deformación tiende a infinito, y la columna se colapsa. Una manera de expresar este resultado es: | |||
::<math>P_{C exacta} =J.\frac{\pi^2.E.I}{4.L^2}</math>; siendo <math>J < 1</math> | |||
El valor del coeficiente corrector <math>J</math> puede estimarse, por ejemplo gracias a una integración numérica, obteniéndose valores situados entre 0,80 y 0,90. | |||
Por estas razones, el cálculo de columnas a partir del razonamiento de <math>Euler</math>, no resulta fiable, dando lugar a resultados de '''carga crítica''' más altos de lo que la realidad experimental muestra. | |||
==Tensión critica== | |||
Se define como ''Tensión Crítica'' (algunos autores hablan de ''Fatiga Critica'') al '''cociente bruto''' entre la carga critica <math>P_C</math> y el área transversal de la barra, columna o elemento. En este caso particular: | |||
::<math>\sigma_C=J\frac{\pi^2.E.I}{4.L^2.A}</math> | |||
Si se define como <math>radio\;de\;giro, i</math> , a la relación: <math>i ={\sqrt{\frac{I}{A}}}</math>, puede escribirse: <math>\sigma_C=J\frac{\pi^2.E}{4.L^2\frac{1}{(\sqrt{\frac{I}{A}})^2}}</math> | |||
Se suele denominar a la relación <math>\lambda=\frac{L}{i}\;Esbeltez\;de\;la\;columna</math>, | |||
con lo que la expresión de la <math>Tension\;Critica</math> quedará finalmente así: <math>\sigma_C=J\frac{\pi^2.E}{4.\lambda^2}</math> | |||
. | . | ||
==Generalización del pandeo de barras prismáticas== | |||
===Caso de una barra con los extremos libres=== | |||
Se trata de estudiar la estabilidad de una barra prismática perfectamente recta, sin ninguna carga transversal. Está articulada en sus dos extremos y uno de ellos puede desplazarse axialmente, lo que permite la compresión de la columna. | |||
Si la barra es perfectamente recta y la carga que la deforma está exactamente en su eje, la barra soportará la carga P/A hasta llegar al límite de fluencia a la compresión. Cualquier ligera imperfección, tanto en la barra como en la aplicación de la carga, provocarán un pandeo en alguna dirección (véase la figura adjunta), con un solo seno (caso a), o dos (b), cuatro (c), etc. Sin embargo, si la carga es inferior a la crítica, esta deformación no implicará ningún colapso de la barra. Por el contrario, si esta carga alcanza el valor crítico <math>P_C</math>, la deformación seguirá indefinidamente, alcanzará el punto de fluencia y la barra se deformará plásticamente (colapso). En función del número de nodos que se generen, la carga crítica toma diferentes valores. | |||
[[Imagen:Pandeo01.jpg|right|250px||]] | |||
En la fórmula ya vista, <math>P_C=\frac{J.\pi^2.E.I}{4.L^2}</math> | |||
la longitud <math>L</math> representa la longitud de una barra que se deforma de tal manera que sólo presenta "medio" seno. En el caso (a), en razón de la simetría de la deformación, la longitud a emplear en la fórmula anterior sería <math>\frac{L}{2}</math>: | |||
::<math>P_C(a)=\frac{J.\pi^2.E.I}{L^2}</math> | |||
Análogamente: | |||
::<math>P_C(b)=\frac{4.J.\pi^2.E.I}{L^2}</math> | |||
::<math>P_C(c)=\frac{8.J.\pi^2.E.I}{L^2}</math>, etc. | |||
== | Es decir que: <math>P_C(a) = 0,25.\;P_C(b) = 0,125,\;P_C(c) </math>.... | ||
En otras palabras, si sobre una barra se aplica una fuerza P que vaya aumentando progresivamente, el primer colapso se obtendrá con una deformación del tipo (a), puesto que deformaciones con más senos exigen mayores esfuerzos, a los que no se llegará puesto que el colapso se alcanzará antes. | |||
===Barra empotrada en ambos extremos=== | |||
[[Imagen:Pandeo02.jpg|left|80px||]] | |||
En razón de la homogeneidad del material y de la simetría del conjunto, la deformación se producirá de tal manera que la deformada puede dividirse en cuatro partes iguales, cuya figura será igual a la de la columna anteriormente estudiada, presentando tres puntos en los que ::<math> \frac{dx}{dy} = 0</math>. | |||
La carga crítica, en este caso, coincide con la de una columna biarticulada de longitud <math>L/2</math>. Por lo tanto el pandeo de la columna biempotrada se produce por colapso en la zona central de longitud <math>L/2</math>, que se comporte como biarticulada: | |||
::<math>P_C = \frac{4.J.\pi^2.E.I}{L^2}</math> | |||
===Barra empotrada y articulada en un extremo=== | |||
[[Imagen:Pandeo03.jpg|right|60px||]] | |||
Este caso es similar al de una columna biarticulada de longitud <math>L/2</math>. Por lo tanto el pandeo de esta columna se produce por colapso de una zona de longitud aproximadamente de <math>(0.7.L)</math>, que se comporta como biarticulada: | |||
::<math>P_C = \frac{J.\pi^2.E.I}{(0,7.L)^2}</math> | |||
===Fórmula general=== | |||
A la vista de estos resultados, puede presentarse como fórmula generalizada de la ''Tensión Crítica'' la expresión | |||
::<math>P_C = \frac{J.\pi^2.E.I}{(\zeta.L)^2}</math> | |||
El número <math>\zeta</math> depende de la forma que adopte la deformada, en función de los tipos de fijación de sus extremos. | |||
<math>J</math> es el factor corrector debido a la integración simplificada de la ecuación diferencial de la elástica. | |||
Al producto <math>L_P =\zeta.L</math> se le suele denominar ''Longitud equivalente de pandeo''. | |||
El | |||
La ''Esbeltez equivalente de pandeo'' viene dada por la expresión <math>\lambda = \frac{L_P}{i} = \frac{\zeta.L}{i}</math> | |||
===Los "coeficientes de seguridad"=== | |||
El tratamiento teórico del problema (resuelto de una manera aproximada, como se ha visto), así como las incertidumbre sobre el cumplimiento de las hipótesis iniciales en la práctica industrial, especialmente en lo referente a la homogeneidad y respeto a las cuestiones dimensionales, han aconsejado la aplicación de sistemas de cálculo, que si bien se apoyan cualitativamente en la teoría ya expuesta, intentan dar satisfacción a los resultados prácticos y experimentales observados para garantizar construcciones sólidas y estables. | |||
La primera aproximación se obtiene simplemente aplicando un coeficiente de seguridad de 0,5 a los valores obtenidos por la teoría, en particular en lo referente a la "Carga crítica". El sistema es excesivamente simple y poco fiable en caso de barras formando parte de sistemas complejos. | |||
==Las fórmulas empíricas== | |||
Diferentes ingenieros y asociaciones han propuesto distintas fórmulas, de origen exclusivamente empírico, para el cálculo de barras y columnas sometidas a esfuerzos de compresión. Entre las más clásicas, merecen ser mencionadas las primeras de ''Rankine'', para columnas cortas, y de ''Tetmajer'', ambas en desuso. | |||
Recuérdese que: <math>\lambda = \frac{L_P}{i}</math>, y que <math>i = \sqrt{\frac{I}{A}}</math>, | |||
por lo que resulta:<math>\lambda = \frac{L_P}{\sqrt{\frac{I}{A}}}</math> | |||
Como ejemplos ilustrativos se mencionan los siguientes: | |||
::'''Fórmula de Tredgold''' | |||
Es una de las más antiguas. Se la conoce desde 1886. Fue adoptada por ''Gordon'' para representar los resultados experimentales de ''Hodgkinson'', si bien posteriormente fue modificada por ''Rankine''. La '''''tensión media compresora <math>\sigma_U</math> admitida''''', según este autor, deberá ser: | |||
::<math>\sigma_U = \frac{a}{1 + b.\lambda^2}</math> | |||
siendo <math>a</math> y <math>b</math> dos constantes, función del material utilizado. El Instituto ''Americano para la Construcción en Acero'' en 1928 la expresó así: | |||
<math>\ | ::<math>\lambda > 60, \;\;\sigma_U = \frac{18.000}{1 + \frac{\lambda^2}{18.000}}\;libras/pulgada^2</math> | ||
<math>\ | ::<math>\lambda < 60,\;\;\sigma_U = 15.000\;libras/pulgada^2</math> | ||
::'''Fórmula de Ostenfeld''' | |||
Data de 1898. La ''Fatiga Crítica'' para el acero de construcción, según este autor, se expresa así: | |||
<math> | ::<math>\sigma_{CR} = 2.650 - 0,09.\lambda^2\;kg/cm^2</math> | ||
<math> | Esta parábola es tangente a la curva de Euler en <math>\lambda = 122,5</math> y da lugar a | ||
<math>\sigma_{CR} = 2.650\;kg/cm^2</math>. Los coeficientes de seguridad a adoptar, según Ostenfeld, | |||
se sitúan entre <math>2,5\;y\;3</math>. | |||
::'''Fórmula de la Asociación Americana de Ingenieros de Ferrocarriles''' | |||
En este caso, las fórmulas se refieren a la ''Fatiga admitida'' <math>\sigma_U</math>. | |||
::<math>30 < \lambda < 120\;y\;piezas\;principales:\;\sigma_U = 16.000 - 70.\lambda\;libras/pulgada^2</math> | |||
::<math>30 < \lambda < 150\;y\;piezas\;secundarias:\;\sigma_U = 16.000 - 70.\lambda\;libras/pulgada^2</math> | |||
::<math>\lambda < 30:\;\;\sigma_U = 14.000\;libras/pulgada^2</math> | |||
::'''Fórmula del Column Research Council (CRC)''' | |||
Aplicable solamente para barras y columnas de acero. | |||
En todo lo que sigue, <math>\sigma_{CR}</math> representa '''el valor límite o "Crítico" de la tensión media P/A. | |||
<math> | Se define a: <math>\lambda_{CR} = \sqrt{\frac{2.\pi^2.E}{\sigma_F}}</math> que, según esta organización, fija el límite entre el pandeo elástico e inelástico. | ||
<math> | Según el valor de <math>\lambda</math> de la columna de acero se aplicará: | ||
<math>\lambda < \lambda_{CR}:\;\; \frac{\sigma_{CR}}{\sigma_F} = 1 - 0,5.(\frac{\lambda}{\lambda_{CR}})^2</math> | |||
<math> | <math>\lambda > \lambda_{CR}:\;\;\frac{\sigma_{CR}}{\sigma_F} = 0,5.(\frac{\lambda_{CR}}{\lambda})^2</math> | ||
::'''Fórmula del Structural Stability Research Council (SSRC)''' | |||
Este organismo propuso en 1976, como consecuencia de sus resultados experimentales, un conjunto de fórmulas distintas, según material, tipo de perfil y proceso de fabricación. De entre todas ellas, la más utilizada para construcciones de acero es la denominada ''nº 2''. | |||
<math>E</math>: | Definiendo a <math>\mu = \lambda.\sqrt{\frac{\sigma_F}{\pi^2.E}}</math>, se aplican las siguientes reglas: | ||
<math> | <math>0 < \mu < 0,15:\;\;\frac{\sigma_{CR}}{\sigma_F} = 1</math> | ||
<math> | <math>0,15 < \mu < 1,0:\;\;\frac{\sigma_{CR}}{\sigma_F} = 1,035 - 0,202.\mu - 0,222.\mu^2</math> | ||
<math> | <math>1,0 < \mu < 2,0:\;\;\frac{\sigma_{CR}}{\sigma_F} = -0,111 + \frac{0,636}{\mu} + \frac{0,087}{\mu^2}</math> | ||
<math>2,0 < \mu < 3,6:\;\;\frac{\sigma_{CR}}{\sigma_F} = 0,009 + \frac{0,877}{\mu^2}</math> | |||
<math>\mu > 3,6:\;\;\frac{\sigma_{CR}}{\sigma_F} = \frac{1}{\mu^2}</math> | |||
::'''Fórmula del American Institute of Steel Contruction (AISC)''' | |||
En 1986 este organismo modifica la fórmula nº 2 anterior para columnas de edificios, de la manera siguiente: | |||
= | <math>\mu < 1,5:\;\;\frac{\sigma_{CR}}{\sigma_F} =e^{-0,419.\mu^2}</math> | ||
<math>\mu > 1,5:\;\;\frac{\sigma_{CR}}{\sigma_F} =\frac{0,877}{\mu^2}</math> | |||
==Sistemas semiempíricos== | |||
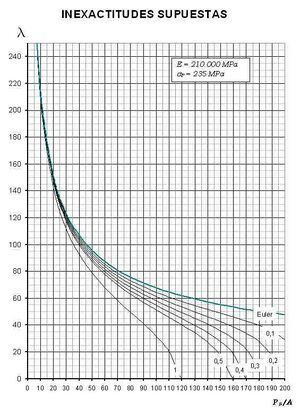
===Método de las "inexactitudes supuestas"=== | |||
[[Imagen:PandeoIS.jpg|left|300px||]] | |||
Una columna empotrada en un extremo, sometida a un esfuerzo axial (pandeo) sufre una deformación, provocada por un momento flector cuyo valor máximo. según se ya se vio en el ejemplo inicial, valía: <math>M_{Max} = -P.(d+e) = -P.e.sec (\sqrt{\frac{P}{E.I}}.L)</math> | |||
Puesto que, en general, <math>\sigma = \frac{M}{h.I}</math>, en este caso sería: | |||
::<math>\sigma_{Max} = \frac{P}{A} + \frac{P.e.h.sec (\sqrt{\frac{P}{E.I}}.L}{I})</math> | |||
Puede ocurrir que antes de que la carga <math>P</math> provoque una deformación de colapso, la fatiga máxima en el empotramiento alcance su valor de fluencia, y el colapso de la pieza no se produzca por la deformación crítica, sino por haberse alcanzado antes, en la fibra más cargada, el valor de fluencia <math>\sigma_F</math>. En este caso, la carga crítica vendrá definida por la expresión: | |||
::<math>\sigma_F < \frac{P_F}{A}.(1+ \frac{P_F.e.h.sec (\frac{L}{i}.\sqrt{\frac{P_F}{E.A}}}{I})</math> | |||
en la que figura la excentricidad de origen <math>e</math>, a la que podemos reducir a su valor adimensional, poniendo: <math>\xi = \frac{e.h.A}{I}</math> | |||
Esta excentricidad de origen deba ser considerada como una inexactitud propia de la fabricación del perfil y/o de la aplicación de la carga: | |||
::<math>\sigma_F < \frac{P_F}{A}.(1+ \xi.sec (\lambda.\sqrt{\frac{P_F}{E.A}})</math> | |||
<math> | A partir de esta fórmula resulta inmediato calcular, con la ayuda del ábaco adjunto, el valor límite de <math>P_F</math> en función de la excentricidad relativa inicial <math>\xi</math> de la columna o barra sometidas a compresión. | ||
Si la barra está articulada en sus extremos, no debe olvidarse que el valor <math>L</math> que figura en la fórmula debe ser la mitad de la distancia entre los dos extremos articulados. Calculado el valor límite <math>P_F</math>, se le aplicará un coeficiente de seguridad (generalmente 0,5) para obtener la carga de uso admisible <math>P_U</math>. | |||
La definición de las inexactitudes originales para cada perfil de barra o columna se realizará mediante la experimentación. | |||
===Método del coeficiente de pandeo <math>\omega</math>=== | |||
Este método es de aplicación muy sencilla, y ha sido adoptado por varias normas, entre ellas la MV103 (Dutheil). Consiste sencillamente en multiplicar la tensión nominal de trabajo de la columna por un coeficiente denominado coeficiente de pandeo <math>\omega</math>, superior a la unidad, de tal forma que el producto resultante sea inferior al límite elástico, o la tensión de diseño del material en su caso. | |||
<math>\ | Por lo tanto, en el límite antes de producirse el pandeo se debe cumplir: | ||
::<math>\omega.\sigma_{CR} < \sigma_U</math> | |||
= | Recuérdese que <math>\sigma_E = \frac{\pi^2.E}{\lambda^2}</math> y que <math>\sigma_F</math> es la tensión de fluencia del acero | ||
<math> | ::<math>\omega = 0,5 + 0,65.\frac{\sigma_F}{\sigma_E} + \sqrt{(0,5 + 0,65.\frac{\sigma_F}{\sigma_E})^2 - \frac{\sigma_F}{\sigma_E}}</math> | ||
===Norma NBE-EA-95=== | |||
Esta norma está establecida para Estructuras de Acero en Edificación y se apoya en los conceptos del caso anterior. | |||
Comprende un conjunto de recomendaciones, a saber: | |||
::'''a) Norma sobre los espesores de los planos de las piezas comprimidas''' | |||
Cada elemento plano de una pieza comprimida tendrá espesor suficiente para que no sufra abolladura antes del agotamiento de la pieza, por pandeo del conjunto. Se considera que un elemento plano de cualquier tipo de acero tiene espesor suficiente, si cumple la limitación: | |||
::<math>\frac{h}{e} < \eta.\sqrt{\frac{2.400}{\sigma_U}}</math> | |||
con el valor de <math>\eta</math> que se establece en la tabla correspondiente del ''Prontuario de Estructuras Metálicas''. | |||
::'''b) Cálculo a pandeo de piezas sometidas a compresión''' | |||
::<math>\omega = 0,5 + 0,65.\frac{\sigma_F}{\sigma_E} + \sqrt{(0,5 + 0,65.\frac{\sigma_F}{\sigma_E})^2 - \frac{\sigma_F}{\sigma_E}}</math> | |||
::<math>Coeficientes\;a\;utilizar\;para\;aceros</math> | |||
::<math>|\;Tipo\;\;|\;\sigma_F\;(E = 2.10^{11}Pa)\;|</math> | |||
::<math>\;A 37\;\;\;\;\;\; 228,5 \;MPa</math> | |||
::<math>\;A 42\;\;\;\;\;\; 247,3 \;MPa</math> | |||
::<math>\;A 52\;\;\;\;\;\; 342,9 \;MPa</math> | |||
==='''EUROCÓDIGO 3'''=== | |||
Esta norma se refiere exclusivamente a las construcciones metálicas. | |||
a) | :a) Clasificación de las secciones | ||
EUROCÓDIGO 3 clasifica las secciones de las barras que forman parte de una estructura metálica en cuatro Clases, numeradas del 1 al 4, según la forma de las alas de estos elementos, si están bajo compresión pura, flexión pura o una combinación entre ambas. Se definen las cuatro clases de secciones, de la siguiente forma: | |||
:::*Clase 1: Las secciones transversales en las que se puede formar una rótula plástica con la capacidad de giro requerida para un análisis plástico. | |||
:::*Clase 2: Las secciones transversales en las que se puede alcanzar el momento plástico, pero tiene una capacidad de giro limitada. | |||
:::*Clase 3: Las secciones transversales en las que la tensión de la fibra más comprimida de la pieza puede alcanzar el límite elástico y en las que la abolladura local puede impedir alcanzar el momento plástico. | |||
:::*Clase 4: Las secciones transversales en las que para determinar su resistencia a momento flector o a la compresión, es necesario tener en cuenta explícitamente los efectos locales de abolladura. | |||
La clasificación depende del coeficiente <math>\epsilon</math> que queda definido así: <math>\epsilon = \sqrt{\frac{235}{\sigma_U}} | |||
</math>. | |||
si <math>c</math> es la altura interior de la pieza (medida perpendicularmente ala eje de flexión o pandeo) y <math>t</math> su espesor, puede realizarse una estimación de la categoría a partir de la siguientes reglas: | |||
:::<math>Clase \;1: \;\;\frac{c}{t} < 33.\epsilon</math> | |||
:::<math>Clase \;2: \;\; \frac{c}{t} < 38.\epsilon</math> | |||
:::<math>Clase \;3: \;\; \frac{c}{t} < 42.\epsilon</math> | |||
'''La Clase 4 no se incluye en este estudio, y debe ser tratada de forma especial.''' | |||
<math> | :b) Resistencia a la compresión | ||
Se denomina Resistencia a la Compresión (<math>N_C</math>) a la fuerza axial admisible sin riesgo, aplicable a una columna prismática metálica (comúnmente, de acero laminado). | |||
<math>N_{b,Rd} = \frac{\chi_{min}.A.\beta_A\sigma_F}{\gamma_{M1}}</math> | |||
<math>\chi_{min} = \;coeficiente\;definido\;mas\;abajo</math> | |||
<math>Para\;las\;Clases\;1,\;2\;y\;3\;siempre\;\beta_A = 1</math> | |||
<math>A = area\;seccion\;recta</math> | |||
<math>\sigma_F = tension\;de\;fluencia</math> | |||
<math>\gamma_{M1} = coeficiente\;seguridad\;global\;(generalmente\;1\le \gamma_{M1} \le 1,1)</math> | |||
Frecuentemente la barra sometida a compresión presenta dos ejes de flexión posibles (según <math>x</math> y según <math>y</math>). Para cada uno de ellos se calculará la ''Esbeltez reducida'': | |||
Esbeltez reducida, según <math>x:\;\;\bar \lambda_x = \frac{L}{\pi.i_x.\sqrt{\frac{E}{\sigma_F}}}</math> | |||
Esbeltez reducida, según <math>y:\;\;\bar \lambda_y = \frac{L}{\pi.i_y.\sqrt{\frac{E}{\sigma_F}}}</math> | |||
El coeficiente <math>\chi</math> se determina de acuerdo con el siguiente algoritmo: | |||
::<math>\phi = 0,5.[1 + \alpha.(\bar \lambda - 0,2) + \bar \lambda^2)]</math> | |||
::<math>\chi = \frac{1}{\phi+\sqrt{\phi^2-\bar \lambda^2}}</math> | |||
::<math>Si\;\;\chi > 1\;entonces\;\chi = 1</math> | |||
a) El valor de <math>\bar \lambda</math> que debe tomarse es aquel que haga a <math>\chi</math> menor (<math>\chi_{min}</math>) | |||
b) <math>\alpha</math> es el llamado ''Factor de imperfección'', que depende del tipo de perfil utilizado. Se distribuye según cuatro categorías, que se indican a continuación. | |||
Categorías Ver [[Factor de imperfeccion]] | |||
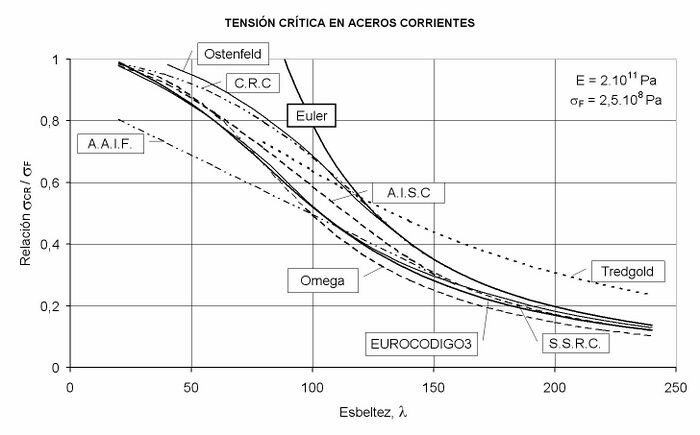
==Comparación entre los diferentes métodos de cálculo de barras sometidas a compresión== | |||
[[Imagen:Pandeo04.jpg|center|700px||]] | |||
<math> | Recuérdese que el valor de la carga axial admitida para una barra o columna dada <math>(P_U)</math>, se obtiene del producto: | ||
<math> | :::<math>P_U = \sigma_{CR}.A.(Coeficiente\;de\;Seguridad)</math> | ||
Este '''Coeficiente de Seguridad''' suele tomarse igual a 0,5. | |||
=Artículos Relacionados= | =Artículos Relacionados= | ||
*[[:Categoría:Cálculo de Estructuras de Acero|Cálculo de Estructuras de Acero: Conceptos Generales]] | *[[:Categoría:Cálculo de Estructuras de Acero|Cálculo de Estructuras de Acero: Conceptos Generales]] | ||
*[[Cálculo de Estructuras de Acero: Caso de | *[[Cálculo de Estructuras de Acero: Caso de las Vigas]] | ||
Revisión actual del 08:59 7 may 2009
Área de Cálculo |
Nota: Este artículo ha sido creado gracias a Área de Cálculo en el marco del Programa de Afiliados de la Construpedia. Ver todos los artículos de Área de Cálculo en la Construpedia.
|
|---|
Los esfuerzos axiales (Pandeo de barras o columnas)
Generalidades
En el análisis lineal de estructuras, a un aumento de las cargas exteriores corresponde un aumento proporcional de las deformaciones y de los esfuerzos internos. Sin embargo, se presentan casos en los que la aplicación de las cargas, aun siendo estas no muy grandes, modifican de tal forma la geometría del sistema, que aquella proporcionalidad deja de ser aplicable, y la estructura se deforma de una manera distinta de lo que correspondería a dichas cargas en el rango lineal, pudiendo incluso provocar su colapso. A los valores de las cargas que provocan el colapso de la estructura, se les denominan cargas críticas de colapso.
Cuando las deformaciones no son pequeñas, la posición de las cargas en la estructura deformada, no puede confundirse con la posición en la estructura sin deformar y por lo tanto, las ecuaciones de equilibrio deben ser planteadas ahora en la posición deformada, y no en la inicial.
Los conceptos de carga crítica y estabilidad del equilibrio pueden ponerse de manifiesto con gran facilidad mediante un caso sencillo, que además permitirá una generalización posterior.
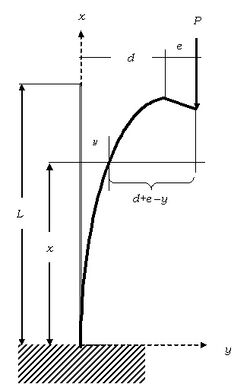
Considérese el sistema mostrado en la figura adjunta. Un análisis de primer orden, planteando el equilibrio en la posición indeformada, indica que la barra está sometida a una compresión simple de valor .
En este caso la flecha no puede despreciarse al lado de la excentricidad inicial . El momento flector a lo largo del eje para cualquier sección se expresará como:
La ecuación general de la deformada –también llamada ecuación de la elástica– se presenta así:
Aplicándola al caso particular en estudio, la integración analítica de esta ecuación, resuelta por Lagrange, conduce a una solución complicada y de engorroso manejo. Schneider deduce para la máxima deformación:
que no deja de ser todavía de manejo engorroso. Por esta razón, algunos autores prefieren la integración de la forma simplificada:
aduciendo que, en la práctica, el valor de: es siempre despreciable. Esta hipótesis puede proporcionar resultados de cierto valor cualitativo y orientativo, si bien su validez numérica, por lo ya expresado, es muy discutible. Aceptada esta hipótesis, la integración de esta última expresión, conduce a:
Cuando el valor de
en la ecuación anterior, la deformación tiende a infinito, lo que significa que la columna se colapsará, es decir, su deformación aumentará hasta que se quede doblada sobre si misma. Antes de llegar a ello, la pieza de acero laminado habrá alcanzado su punto de fluencia, e iniciará una deformación plástica, pudiendo llegar a su límite de rotura. Aceptada esa hipótesis, la carga P que causará este colapso se deducirá de
Al valor de la carga se la denomina .
El momento flector máximo producido por esta carga, se presentará en el empotramiento, y valdrá, según se ha visto:
Observaciones a la definición de Carga Crítica
La integración de la ecuación simplificada no representa, como ya se ha indicado, la solución exacta, ya que si la carga se acerca al valor crítico , las deformaciones son importantes (se "acercan a infinito") y el término no puede ser despreciado. Sin embargo, el resultado exacto de esa integración muestra que la conclusión obtenida en el caso particular anterior, es válida en su aspecto cualitativo y en efecto, cuando la carga toma un cierto valor –aunque inferior al anteriormente denominado crítico– la deformación tiende a infinito, y la columna se colapsa. Una manera de expresar este resultado es:
- ; siendo
El valor del coeficiente corrector puede estimarse, por ejemplo gracias a una integración numérica, obteniéndose valores situados entre 0,80 y 0,90.
Por estas razones, el cálculo de columnas a partir del razonamiento de , no resulta fiable, dando lugar a resultados de carga crítica más altos de lo que la realidad experimental muestra.
Tensión critica
Se define como Tensión Crítica (algunos autores hablan de Fatiga Critica) al cociente bruto entre la carga critica y el área transversal de la barra, columna o elemento. En este caso particular:
Si se define como , a la relación: , puede escribirse:
Se suele denominar a la relación ,
con lo que la expresión de la quedará finalmente así: .
Generalización del pandeo de barras prismáticas
Caso de una barra con los extremos libres
Se trata de estudiar la estabilidad de una barra prismática perfectamente recta, sin ninguna carga transversal. Está articulada en sus dos extremos y uno de ellos puede desplazarse axialmente, lo que permite la compresión de la columna.
Si la barra es perfectamente recta y la carga que la deforma está exactamente en su eje, la barra soportará la carga P/A hasta llegar al límite de fluencia a la compresión. Cualquier ligera imperfección, tanto en la barra como en la aplicación de la carga, provocarán un pandeo en alguna dirección (véase la figura adjunta), con un solo seno (caso a), o dos (b), cuatro (c), etc. Sin embargo, si la carga es inferior a la crítica, esta deformación no implicará ningún colapso de la barra. Por el contrario, si esta carga alcanza el valor crítico , la deformación seguirá indefinidamente, alcanzará el punto de fluencia y la barra se deformará plásticamente (colapso). En función del número de nodos que se generen, la carga crítica toma diferentes valores.
En la fórmula ya vista, la longitud representa la longitud de una barra que se deforma de tal manera que sólo presenta "medio" seno. En el caso (a), en razón de la simetría de la deformación, la longitud a emplear en la fórmula anterior sería :
Análogamente:
- , etc.
Es decir que: ....
En otras palabras, si sobre una barra se aplica una fuerza P que vaya aumentando progresivamente, el primer colapso se obtendrá con una deformación del tipo (a), puesto que deformaciones con más senos exigen mayores esfuerzos, a los que no se llegará puesto que el colapso se alcanzará antes.
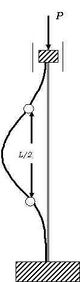
Barra empotrada en ambos extremos
En razón de la homogeneidad del material y de la simetría del conjunto, la deformación se producirá de tal manera que la deformada puede dividirse en cuatro partes iguales, cuya figura será igual a la de la columna anteriormente estudiada, presentando tres puntos en los que ::.
La carga crítica, en este caso, coincide con la de una columna biarticulada de longitud . Por lo tanto el pandeo de la columna biempotrada se produce por colapso en la zona central de longitud , que se comporte como biarticulada:
Barra empotrada y articulada en un extremo
Este caso es similar al de una columna biarticulada de longitud . Por lo tanto el pandeo de esta columna se produce por colapso de una zona de longitud aproximadamente de , que se comporta como biarticulada:
Fórmula general
A la vista de estos resultados, puede presentarse como fórmula generalizada de la Tensión Crítica la expresión
El número depende de la forma que adopte la deformada, en función de los tipos de fijación de sus extremos.
es el factor corrector debido a la integración simplificada de la ecuación diferencial de la elástica.
Al producto se le suele denominar Longitud equivalente de pandeo.
La Esbeltez equivalente de pandeo viene dada por la expresión
Los "coeficientes de seguridad"
El tratamiento teórico del problema (resuelto de una manera aproximada, como se ha visto), así como las incertidumbre sobre el cumplimiento de las hipótesis iniciales en la práctica industrial, especialmente en lo referente a la homogeneidad y respeto a las cuestiones dimensionales, han aconsejado la aplicación de sistemas de cálculo, que si bien se apoyan cualitativamente en la teoría ya expuesta, intentan dar satisfacción a los resultados prácticos y experimentales observados para garantizar construcciones sólidas y estables.
La primera aproximación se obtiene simplemente aplicando un coeficiente de seguridad de 0,5 a los valores obtenidos por la teoría, en particular en lo referente a la "Carga crítica". El sistema es excesivamente simple y poco fiable en caso de barras formando parte de sistemas complejos.
Las fórmulas empíricas
Diferentes ingenieros y asociaciones han propuesto distintas fórmulas, de origen exclusivamente empírico, para el cálculo de barras y columnas sometidas a esfuerzos de compresión. Entre las más clásicas, merecen ser mencionadas las primeras de Rankine, para columnas cortas, y de Tetmajer, ambas en desuso.
Recuérdese que: , y que ,
por lo que resulta:
Como ejemplos ilustrativos se mencionan los siguientes:
- Fórmula de Tredgold
Es una de las más antiguas. Se la conoce desde 1886. Fue adoptada por Gordon para representar los resultados experimentales de Hodgkinson, si bien posteriormente fue modificada por Rankine. La tensión media compresora admitida, según este autor, deberá ser:
siendo y dos constantes, función del material utilizado. El Instituto Americano para la Construcción en Acero en 1928 la expresó así:
- Fórmula de Ostenfeld
Data de 1898. La Fatiga Crítica para el acero de construcción, según este autor, se expresa así:
Esta parábola es tangente a la curva de Euler en y da lugar a . Los coeficientes de seguridad a adoptar, según Ostenfeld, se sitúan entre .
- Fórmula de la Asociación Americana de Ingenieros de Ferrocarriles
En este caso, las fórmulas se refieren a la Fatiga admitida .
- Fórmula del Column Research Council (CRC)
Aplicable solamente para barras y columnas de acero. En todo lo que sigue, representa el valor límite o "Crítico" de la tensión media P/A.
Se define a: que, según esta organización, fija el límite entre el pandeo elástico e inelástico.
Según el valor de de la columna de acero se aplicará:
- Fórmula del Structural Stability Research Council (SSRC)
Este organismo propuso en 1976, como consecuencia de sus resultados experimentales, un conjunto de fórmulas distintas, según material, tipo de perfil y proceso de fabricación. De entre todas ellas, la más utilizada para construcciones de acero es la denominada nº 2.
Definiendo a , se aplican las siguientes reglas:
- Fórmula del American Institute of Steel Contruction (AISC)
En 1986 este organismo modifica la fórmula nº 2 anterior para columnas de edificios, de la manera siguiente:
Sistemas semiempíricos
Método de las "inexactitudes supuestas"
Una columna empotrada en un extremo, sometida a un esfuerzo axial (pandeo) sufre una deformación, provocada por un momento flector cuyo valor máximo. según se ya se vio en el ejemplo inicial, valía:
Puesto que, en general, , en este caso sería:
Puede ocurrir que antes de que la carga provoque una deformación de colapso, la fatiga máxima en el empotramiento alcance su valor de fluencia, y el colapso de la pieza no se produzca por la deformación crítica, sino por haberse alcanzado antes, en la fibra más cargada, el valor de fluencia . En este caso, la carga crítica vendrá definida por la expresión:
en la que figura la excentricidad de origen , a la que podemos reducir a su valor adimensional, poniendo:
Esta excentricidad de origen deba ser considerada como una inexactitud propia de la fabricación del perfil y/o de la aplicación de la carga:
A partir de esta fórmula resulta inmediato calcular, con la ayuda del ábaco adjunto, el valor límite de en función de la excentricidad relativa inicial de la columna o barra sometidas a compresión.
Si la barra está articulada en sus extremos, no debe olvidarse que el valor que figura en la fórmula debe ser la mitad de la distancia entre los dos extremos articulados. Calculado el valor límite , se le aplicará un coeficiente de seguridad (generalmente 0,5) para obtener la carga de uso admisible .
La definición de las inexactitudes originales para cada perfil de barra o columna se realizará mediante la experimentación.
Método del coeficiente de pandeo
Este método es de aplicación muy sencilla, y ha sido adoptado por varias normas, entre ellas la MV103 (Dutheil). Consiste sencillamente en multiplicar la tensión nominal de trabajo de la columna por un coeficiente denominado coeficiente de pandeo , superior a la unidad, de tal forma que el producto resultante sea inferior al límite elástico, o la tensión de diseño del material en su caso.
Por lo tanto, en el límite antes de producirse el pandeo se debe cumplir:
Recuérdese que y que es la tensión de fluencia del acero
Norma NBE-EA-95
Esta norma está establecida para Estructuras de Acero en Edificación y se apoya en los conceptos del caso anterior.
Comprende un conjunto de recomendaciones, a saber:
- a) Norma sobre los espesores de los planos de las piezas comprimidas
Cada elemento plano de una pieza comprimida tendrá espesor suficiente para que no sufra abolladura antes del agotamiento de la pieza, por pandeo del conjunto. Se considera que un elemento plano de cualquier tipo de acero tiene espesor suficiente, si cumple la limitación:
con el valor de que se establece en la tabla correspondiente del Prontuario de Estructuras Metálicas.
- b) Cálculo a pandeo de piezas sometidas a compresión
EUROCÓDIGO 3
Esta norma se refiere exclusivamente a las construcciones metálicas.
- a) Clasificación de las secciones
EUROCÓDIGO 3 clasifica las secciones de las barras que forman parte de una estructura metálica en cuatro Clases, numeradas del 1 al 4, según la forma de las alas de estos elementos, si están bajo compresión pura, flexión pura o una combinación entre ambas. Se definen las cuatro clases de secciones, de la siguiente forma:
- Clase 1: Las secciones transversales en las que se puede formar una rótula plástica con la capacidad de giro requerida para un análisis plástico.
- Clase 2: Las secciones transversales en las que se puede alcanzar el momento plástico, pero tiene una capacidad de giro limitada.
- Clase 3: Las secciones transversales en las que la tensión de la fibra más comprimida de la pieza puede alcanzar el límite elástico y en las que la abolladura local puede impedir alcanzar el momento plástico.
- Clase 4: Las secciones transversales en las que para determinar su resistencia a momento flector o a la compresión, es necesario tener en cuenta explícitamente los efectos locales de abolladura.
La clasificación depende del coeficiente que queda definido así: .
si es la altura interior de la pieza (medida perpendicularmente ala eje de flexión o pandeo) y su espesor, puede realizarse una estimación de la categoría a partir de la siguientes reglas:
La Clase 4 no se incluye en este estudio, y debe ser tratada de forma especial.
- b) Resistencia a la compresión
Se denomina Resistencia a la Compresión () a la fuerza axial admisible sin riesgo, aplicable a una columna prismática metálica (comúnmente, de acero laminado).
Frecuentemente la barra sometida a compresión presenta dos ejes de flexión posibles (según y según ). Para cada uno de ellos se calculará la Esbeltez reducida:
Esbeltez reducida, según
Esbeltez reducida, según
El coeficiente se determina de acuerdo con el siguiente algoritmo:
a) El valor de que debe tomarse es aquel que haga a menor ()
b) es el llamado Factor de imperfección, que depende del tipo de perfil utilizado. Se distribuye según cuatro categorías, que se indican a continuación.
Categorías Ver Factor de imperfeccion
Comparación entre los diferentes métodos de cálculo de barras sometidas a compresión
Recuérdese que el valor de la carga axial admitida para una barra o columna dada , se obtiene del producto:
Este Coeficiente de Seguridad suele tomarse igual a 0,5.






![{\displaystyle {\frac {d^{2}y}{dx^{2}}}=-{\frac {M}{E.I}}.[1+({\frac {dy}{dx}})^{2}]^{3/2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e4217277e5e7e8b308975caa6398f661b11a17a1)
![{\displaystyle y_{M}={\sqrt {\frac {E.I}{P}}}{\sqrt {[{\frac {P}{P_{M}}}-1]-{\frac {9}{4}}[{\frac {P}{P_{M}}}-1]^{2}+{\frac {31}{8}}[{\frac {P}{P_{M}}}-1]^{3}-....}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0d419ba005cf030af548bca0bf24e8429e3a1cdf)

![{\displaystyle [1+({\frac {dy}{dx}})^{2}]^{3/2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4535fb49766320b4b62d00fee8356185e029bae8)
![{\displaystyle y={\frac {e.[1-cos({\sqrt {\frac {P}{E.I}}}.x)]}{cos({\sqrt {\frac {P}{E.I}}}.L)}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3401d7c5a53ab2e8618a678bff2ebe6ec3238d7d)





































































































![{\displaystyle \phi =0,5.[1+\alpha .({\bar {\lambda }}-0,2)+{\bar {\lambda }}^{2})]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/16f29d66552fdeac0163b9e417fbe1573ad337e4)