Cálculo de Estructuras de Acero
De Construmatica
Área de Cálculo |
Nota: Este artículo ha sido creado gracias a Área de Cálculo en el marco del Programa de Afiliados de la Construpedia. Ver todos los artículos de Área de Cálculo en la Construpedia.
|
|---|
Para cualquier consulta sobre el contenido, puede dirigirse a Área de Cálculo donde existen una serie de ayudas desarrolladas por un equipo de ingenieros en colaboración con el autor de estos apuntes para el cálculo de elementos de hormigón.
Aceros Laminados (o Estructurales)
Los aceros laminados –también denominados aceros estructurales–, generalmente utilizados para la construcción de estructuras metálicas, son derivados de aleaciones del hierro y carbono. Se producen a partir del arrabio (o hierro en bruto obtenido por la reducción del mineral de hierro en hornos altos) al que se le somete a una serie de tratamientos físico-químicos que le modifican tanto su composición química, como sus propiedades físicas, obteniéndose así diferentes calidades de aceros. A partir de estos, por laminación (ya sea en caliente o en frío), se producen piezas en forma de prisma de sección transversal uniforme, cuya sección puede adoptar diferentes perfiles, desde el simple perfil rectangular (chapas y pletinas) hasta secciones elaboradas en forma de I, de H, de U, de T , angulares, raíles, etc.
Las calidades de los aceros laminados (y por tanto, sus propiedades) están normalizadas en todos los países, si bien no de la misma manera. En España estas calidades se rigen (año 2006) por la Norma UNE 36010.
Algunos conceptos generales
Esfuerzos de Tracción
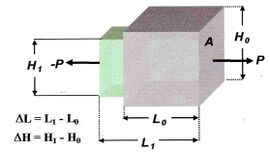
Sometido un cuerpo cualquiera a un esfuerzo (P), llamaremos sección transversal (A) al esfuerzo, a la sección de la pieza, normal al vector fuerza P –es decir, a la dirección de ese esfuerzo–. El cociente = se denomina tensión a la que sometemos a la sección considerada.
El esfuerzo provocado por la fuerza P, producirá una deformación absoluta del cuerpo en cuestión (L) en la dirección de la aplicación de la fuerza. Con respecto a su dimensión inicial , el alargamiento unitario vendrá definido como:
= .
La deformación en el sentido de la fuerza aplicada, no sólo modifica la dimensión en la dirección esta fuerza (en el caso de la Figura 1, alargamiento), sino que también deforma al cuerpo en las direcciones perpendiculares y en el sentido contrario a estas (en el caso de la figura 1, se tratará de un encogimiento de estas dimensiones).
El aumento de longitud en el sentido perpendicular al de la fuerza aplicada será (H'). La variación relativa, respecto de la dimensión inicial , será = .
La relación entre las dos variaciones dimensionales como consecuencia de la aplicación de la fuerza P, se denomina módulo de Poisson: = – .
Esfuerzos Cortantes
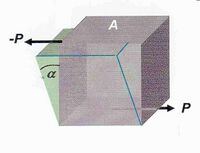
Si sobre un cuerpo la fuerza se aplica de manera tangente, su deformación se efectúa de la manera que se esquematiza en la figura adjunta.
Se dice que la fuerza es una fuerza cortante pura. La deformación producida viene caracterizada por el ángulo , tal y como se esquematiza en la figura.
La tensión se simboliza por la letra , y vale: = .
La Ley de Hooke
Como se verá en el punto siguiente, que los aceros usados para la obtención de piezas laminadas presentan, ante tensiones de extensión (o compresión) inferiores a un cierto valor , una proporcionalidad entre las tensiones () y los alargamientos unitarios (). La constante de proporcionalidad entre ambos parámetros se denomina módulo de elasticidad o también módulo de Young, y suele representarse por la letra E. De manera algebraica, esta proporcionalidad se expresará como: = E•.
Esta expresión se conoce como Ley de Hooke, y sólo es aplicable a ciertos materiales (elásticos de Hooke) y dentro de los límites ya referidos.
Esta ley supone que si la tensión desaparece, la forma del objeto retorna exactamente a la original, o bien, si esta tensión se reduce a la mitad, la deformación (alargamiento o retracción) se reduce igualmente exactamente a la mitad. Es decir, en ella no se contempla ningún fenómeno de histéresis.
De la definición del módulo de Poisson () se deduce: = •, es decir: = •
En el caso de fuerzas cortantes sobre cuerpos elásticos de Hooke, la ley se expresa como: = G•
en la que la constante de proporcionalidad (G) entre deformaciones angulares y tensiones se denomina módulo de elasticidad transversal o módulo de tensión cortante. Esta constante o módulo no es independiente del de Young, sino que está relacionado con él según la relación: G = .
Características mecánicas de los aceros laminados
Las características mecánicas de los aceros, quedan definidas frecuentemente por ensayos mecánicos, entre los que se destacan los siguientes:
Ensayo de tracción
Se realiza sobre probetas generalmente cilíndricas, que sujetas por sus extremos mediante mordazas, en máquinas especiales de ensayo homologadas, son sometidas a un proceso de tracción pura, hasta rotura. Se miden, de manera continua y simultánea las fuerzas de tracción y los alargamientos producidos.
Los detalles del ensayo se encuentran explicitados en las Norma españolas UNE 7117 y siguientes (especialmente las UNE 7474-3 y UNE 7474-5).
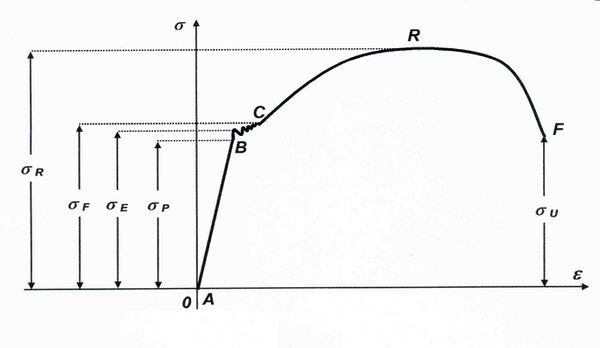
Representando en un diagrama cartesiano los resultados de un ensayo de tracción sobre una probeta de un acero corrientemente usado en la construcción, se obtiene el diagrama esquematizado en la figura 2. En ordenadas se representan las tensiones () o cociente entre la fuerza aplicada P y la sección inicial de la probeta; en abscisas, los alargamientos unitarios (), o cociente entre el alargamiento total y la longitud inicial.
La primera parte de la curva (segmento AB) es prácticamente una recta, que muestra la proporcionalidad entre deformación con respecto a la fuerza aplicada. Si en cualquiera de los puntos entre A y B se anula el esfuerzo, el acero recobra sus dimensiones iniciales Por ello, la tensión correspondiente al punto B, se denomina límite de alargamiento proporcional. El final de la línea oscilante BC, represente el límite de fluencia o límite aparente de elasticidad, y determina el valor . Desde C hasta R los alargamientos se reparten uniformemente en toda la probeta. Para tensiones superiores a , el alargamiento se produce de una manera rápida, con una fuerte reducción de la sección de la probeta, y rotura cuando se alcanza el valor , siempre inferior a . Este ensayo es el que reviste más importancia a los efectos del uso del acero laminado para la construcción de estructuras metálicas.
Ensayo de fatiga
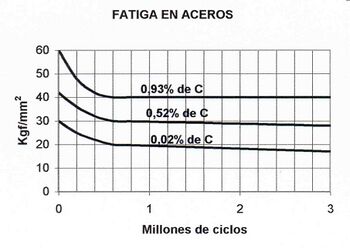
El término fatiga se refiere a la disminución de resistencia mecánica de los aceros por la acción de esfuerzos cíclicos. En las pruebas de fatiga, se somete una probeta a esfuerzos que varían periódicamente de valores positivos a negativos, según diferentes frecuencias. Tras la prueba, se somete a la probeta a un ensayo de resistencia a tracción hasta rotura. Las curvas resultantes de representar la resistencia de cada probeta en función del número de ciclos sufridos presentan un aspecto similar al de la gráfica adjunta. En ella puede observarse como estas curvas tienden asintoticamente a valores de resistencia, denominados tensión de fatiga, que se mantienen para ciclos de hasta 100 o 200 millones de ciclos. La resistencia de estas probetas es inferior a la obtenida sometiendo al acero a cargas aplicadas durante largo tiempo.
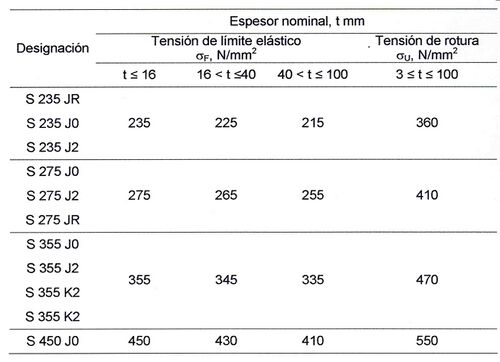
Propiedades mecánicas más relevantes de los Aceros Laminados
Según la Norma UNE EN 10025, las características mínimas deben ser:
Las características siguientes son consideradas como las más comunes a temperatura ambiente, a efectos del cálculo de estructuras en acero laminado:
Módulo de elasticidad (o de Young), E = 210.000
Módulo de Poisson = 0,3 (adimensional)
Módulo de rigidez, G = 81.000
Coeficiente lineal de dilatación térmica, = 1,2·
Densidad, = 7,850
Artículos Relacionados
- Cálculo de Estructuras de Acero: Caso de las Vigas
- Cálculo de Estructuras de Acero: Caso de Esfuerzos Axiales (Columnas)
Enlaces Externos
Subcategorías
Esta categoría contiene las siguientes 3 subcategorías, de un total de 3.
E
Páginas en la categoría «Cálculo de Estructuras de Acero»
Las siguientes 3 páginas pertenecen a esta categoría, de un total de 3.